Теории абсорбции
Когда газ движется турбулентным потоком через поверхность, т. е. Re > 2100, тогда турбулентное перемешивание поддерживает гомогенность состава во всем объеме газа. Ближе к границе раздела фаз движение газа замедляется, и образуются ламинарные слои обычно предполагают, что на границе раздела газ неподвижен.
Наиболее широко известная теория, предполагающая равномерный переход молекул через стабильный пограничный слой, называется теорией двух пленок и была предложена Уайтменом и Льюисом в 1924 г. По этой теории абсорбируемый газ диффундирует через ламинарный пограничный слой и неподвижный "подслой". Если в качестве абсорбента используется жидкость, то существуют такие же пограничные слои со стороны жидкости. Далее предполагают, что на границе раздела жидкость - газ существует равновесие. Тогда парциальное давление pi и концентрация на границе раздела сi взаимосвязаны. Когда достигается состояние установившегося режима переноса, скорость переноса NA из газового потока к границе и от границы раздела в объем жидкости должны быть равны. Тогда
NA = kG (р - рi) = kL (ci - с) (III.23)
где p и pi - парциальное давление переходящего компонента соответственно в объеме газа и на границе; сi и с - концентрация соответственно на границе и в объеме жидкости; kG и kL - коэффициент массопереноса соответственно в газовой и жидкой пленке.
При сравнении с уравнением (III.22) видно, что коэффициент массопереноса в газовой пленке может быть записан в виде
kG = DG/RTx × p/pBM (III.24)
Из уравнения (III.24) следует, что коэффициент массопереноса является функцией коэффициента диффузии, логарифма среднего парциального давления неабсорбирующего компонента и х - расстояния, на котором проходит абсорбция, т. е. толщины пленки. Со стороны пленки жидкости коэффициент массопереноса может быть записан как
kL = DL/XL (III.25)
Где DL - коэффициент диффузии в жидкой фазе; xL - толщина пленки жидкости.
Было показано, что коэффициенты диффузии могут быть рассчитаны, однако толщина пленок не может быть найдена непосредственно. Можно определить эквивалентную толщину пленки с учетом механизма массопереноса через пограничный ламинарный слой из экспериментально найденного коэффициента массопереноса и рассчитанного или (вычисленного коэффициента диффузии. Тогда для абсорбции (подобного типа можно использовать найденное значение. Это было сделано Жильландом и Шервудом, (которые осуществили корреляцию многочисленных экспериментов на колонне пленочного типа
kGRTD/Dv × pBM/p = D/x = 0,023Re0,83Sc0,44 (III.26)
где D - диаметр колонны; Re - число Рейнольдса; Sc - число Шмидта; Dv - коэффициент диффузии в газовой фазе; u - скорость газа относительно колонны; р и μ - плотность и вязкость газа.
Эта корреляция вполне удовлетворительна в тех случаях, когда скорость абсорбции регулируется скоростью переноса через пленку газа, но, к сожалению, из-за колебаний, возникающих в тонком поверхностном слое жидкости, она не может применяться для нахождения эквивалентной толщины пленки в процессах абсорбции, регулируемых скоростью переноса через пленку жидкости.
Если параметром, управляющим системой, является сопротивление пленки жидкости, коэффициент массопереноса может быть измерен на дисковой колонне. При этом получают лучшую корреляцию, чем на пленочной колонне. Коэффициент массопереноса для пленки жидкости kL может быть рассчитан из уравнения:
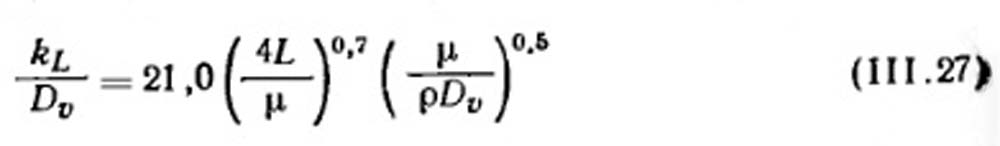
где L - скорость потока жидкости через единицу ширины пленки, кг/(м2×ч).
Однако, даже не имея точных данных о равновесии и коэффициентах переноса для жидкой пленки, можно найти общие коэффициенты массопередачи по уравнению:
NA = КG(р - р*) = KL (с* - с) (III.28)
где р* - равновесное парциальное давление растворимого вещества над раствором, имеющим ту же концентрацию, что и поток жидкости; с* - концентрация раствора, который находился бы в равновесии с растворимым веществом, имеющим то же парциальное давление, что и основной газовый поток.
Эти точки показаны на диаграмме равновесия (рис. III-1).
Общие коэффициенты KG (В единицах давления) и КL (в единицах концентраций) могут быть определены экспериментально, а непосредственно применены в конструкторских расчетах.
Полная движущая сила выражается через (р - р*) в единицах давления и (с* - с) в единицах концентраций. Точка В на равновесной кривой характеризует состав двух фаз на границе раздела, а движущие силы р - pi и сi - с представлены вертикальным отрезком AM и горизонтальным отрезком MB, соответственно.
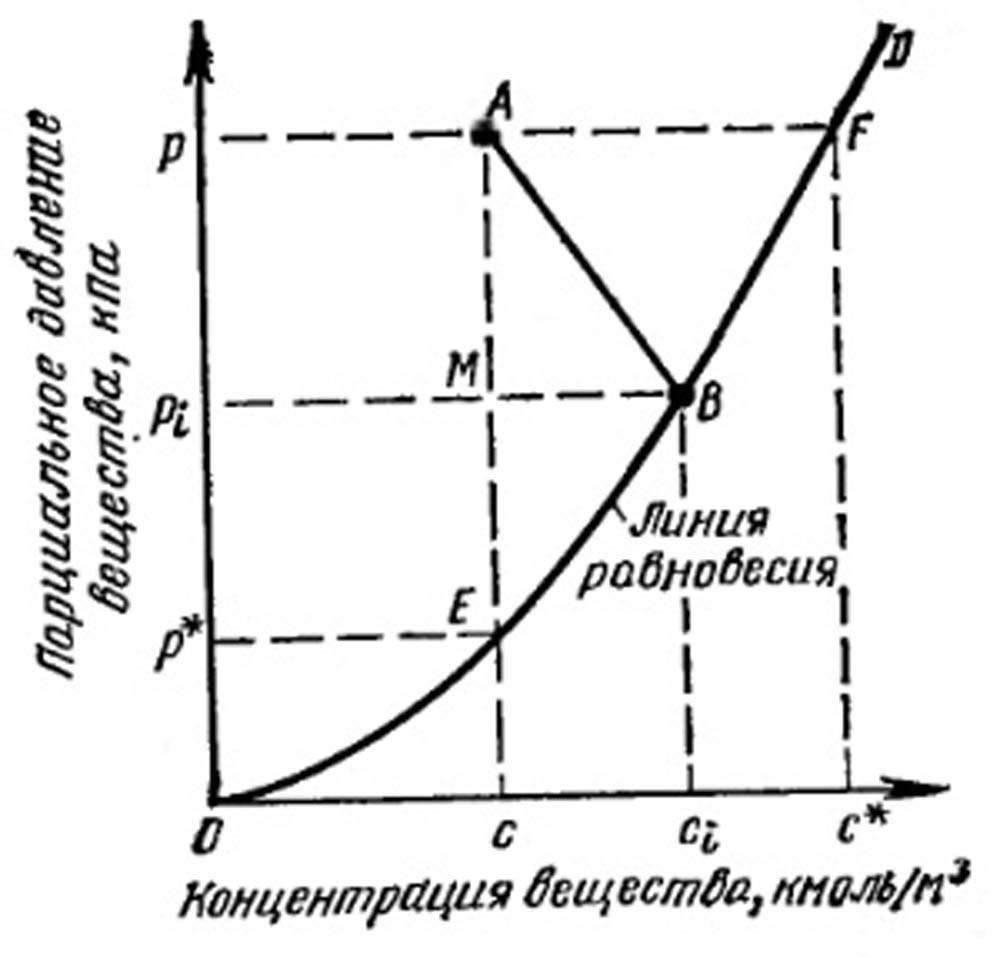
Рис. III-1. Движущие силы процесса абсорбции газов.
Тогда из уравнения (III.23)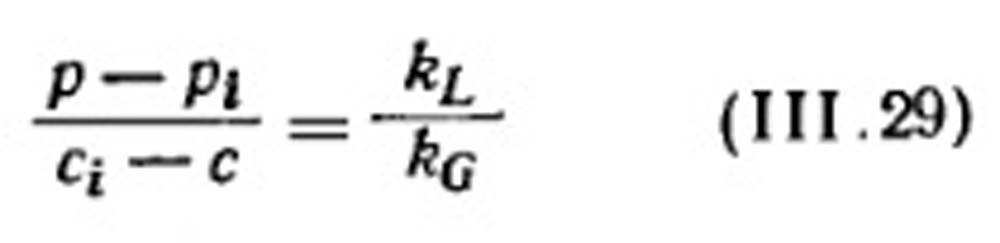
и отношение kL/kG. Представляет наклон прямой АВ. Если уравнение равновесия имеет вид
р* = хс (III.30)
(х - константа), то применим закон Генри. Из уравнений (III.23) и (III.28) можно найти
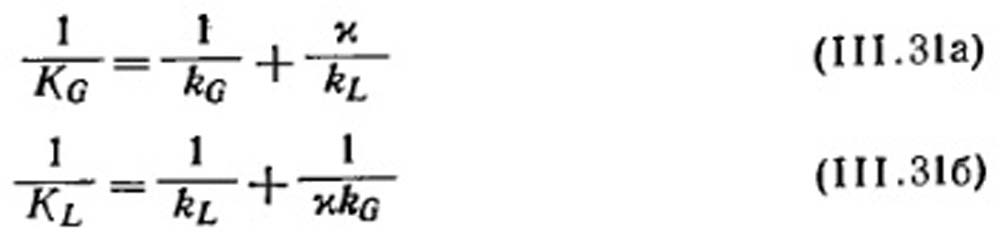
Если x мало, то KG = kG и абсорбция регулируется скоростью переноса через пленку газа, и наоборот, если х велико, то KL = kL и абсорбция регулируется переносом через пленку жидкости.
Уравнение (III.31) показывает также, что при нахождении промежуточных значений коэффициента х необходимо учитывать влияние обеих пленок. Кроме того, если х не является постоянной величиной, т. е. если кривая равновесия не представляет собой прямую, то общие коэффициенты массопередачи будут изменяться при изменении концентрации, так как величина х зависит от концентрации.
Несмотря на то, что теория двух пленок, предложенная Уайтменом - Льюисом, полезна при разработке абсорбционных систем, она заранее предполагает неподвижные пограничные слои и установившийся режим массопереноса, что крайне редко существует в реальных условиях. Так, например, газ стремится разрушить неподвижный слой, и к поверхности жидкости подходит турбулентный поток, тогда как жидкость в поверхностной пленке постоянно заменяется свежей жидкостью снизу. Чтобы исключить проблему диффузии в неустойчивом режиме, в частности, когда взаимодействие газ - жидкость кратковременно, Хигби предложил воображаемую модель, используя уравнение Стефана для молекулярной Диффузии в колонне бесконечной высоты.
Уравнение (III.1), записанное для массопереноса в неустойчивом режиме, было решено для ряда граничных условий. Было установлено, что при данной концентрации в объеме жидкости в начальный период времени существует пограничный слой положительной толщины на границе раздела. В некоторый период времени t уже не существует пограничного слоя, в то время как в объеме жидкости существует бесконечный слой (в соответствии с теорией Стефана). При этом может быть рассчитана концентрация газа ниже поверхности и, кроме того, мгновенная скорость массопереноса газа через единицу поверхности раздела фаз.
NA = 2√п (ci c) Dr (III.32)
Следовательно, мгновенная скорость переноса уменьшается со временем в течение любого периода, пока жидкость остается неподвижной. Общее количество перенесенного вещества можно определить, проинтегрировав уравнение (III.32) по времени, тогда как среднюю скорость переноса можно найти делением этого общего количества на время t. Так, средняя скорость описывается уравнением:
NA = 2(ci - с) √D/пt (III.33)
Это уравнение применимо к абсорбции турбулентного газа в предположении, что после некоторого времени t, в течение которого жидкость неподвижна, происходит легкое перемешивание и этот процесс повторяется бесконечно. Средняя скорость абсорбции в таких условиях описывается уравнением (III.31). Если среднее время t выразить через скорость обновления, определяемую как r = 1/t, то скорость массопереноса можно записать:
NA = 2/√п (ci c) Dr (III.34)
а с учетом уравнения (III.23) получим:
kL = √2/п Dr (III.35)
Необходимо отметить, что хотя это значение kL, по определению, численно равно величине, найденной на основе двухпленочной теории, они имеют различный физический смысл.
Позже Данквертс предложил существенную модификацию модели Хигби, которая заключается в том, что частоту, с которой смешиваются отдельные вертикальные элементы, определяют как r. Затем он предположил, что процесс смешивания, т. е. пребывание (газа у поверхности и частота смешивания, являются случайными процессами. Подобные математические соображения и соответствующие граничные условия могут быть применены для определения скорости массопереноса, которая выражается в виде
NA = (ci - с)Dr (III.36)
kL = Dr' (III.37)
где r' - средняя скорость обмена, которая отличается от "скорости обновления" на коэффициент 2/п.
Модель проникновения Данквертса, примененная к слою жидкости глубиной Н, описывается уравнением
kL = Dr tanh √r Н2D (III.38)
Поскольку член √rН2D тем больше, чем глубже проникновение, значение kL приближается к "бесконечной" глубине по элементарной теории Данквертса.