Электростатические силы

Электростатические силы

В теориях аэродинамического захвата частиц, рассмотренных в предыдущих разделах, не обсуждался вопрос о влиянии электрических зарядов на частице, на пылеуловителе либо на обоих. Тот факт, что электростатические силы могут способствовать фильтрованию, установлен в 30-х годах, и это привело к созданию пропитанных смолой фильтров с повышенной эффективностью. В последние годы внимание исследователей было обращено на выбор фильтровальных тканей с наилучшими электростатическими свойствами для улавливания специфических пылей применялось также механическое нанесение заряда.

Электростатические силы могут быть нанесены на фильтровальную ткань при трении, например, при натирании тканью люситовой полочки или путем пропускания через ткань запыленного газового потока. Когда поток воздуха проходит через фильтр из синтетического волокна со скоростью 1,7 - 2,0 м/с, возникает заряд около 1,2 кВ.

Анализ влияния электростатических сил и их сочетания с основными механизмами аэродинамического захвата чрезвычайно труден. Известны две попытки решения этой проблемы, увенчавшиеся некоторым успехом. Джиллеспай применил подход Лэнгмюра для захвата частиц с учетом электростатических зарядов, возникающих при перехвате или в процессе диффузии частиц, а также использовал условия ламинарности для оценки скоростей потока при его прохождении через фильтр. Результирующие уравнения очень сложны и не будут приведены в настоящей работе.

Более практическими являются графические решения, предложенные Кремером и Джонстоном Расчеты основаны на том, что либо частицы аэрозоля, либо фильтр, либо оба вместе несут заряд (электростатические силы).

Эффективность улавливания была найдена с помощью ЭЦВМ решением уравнений потенциального и вязкого потока.

Существует четыре вида действия электростатических сил в системе частиц, подходящих к пылеуловителю, которые следует учитывать.

• И частицы, и пылеуловитель заряжены, действуют кулоновские силы притяжения или отталкивания в зависимости от относительных знаков зарядов частиц и фильтра. Заряды рассматриваются как точечные. Кулоновская сила имеет величину F_EC.
• Коллектор, несущий заряд, индуцирует на поверхности частиц заряд, противоположный по знаку заряду коллектора. Кулоновская сила величиной F_EI является еще одной внешней силой, действующей на частицы.
• Частица заряжена и, в свою очередь, индуцирует на коллекторе заряд, противоположный по знаку. Таким образом возникает сила F_EM, представляющая собой, как и в предыдущем случае, силу дополнительного взаимодействия между частицей и коллектором.

Частицы несут заряд одного и того же знака и отталкиваются друг от друга с силой F_ES. Это явление называется эффектом, пространственного заряда.

Сила Е между заряженной частицей аэрозоля и заряженным сферическим коллектором (при постоянном заряде) определяется из выражения:

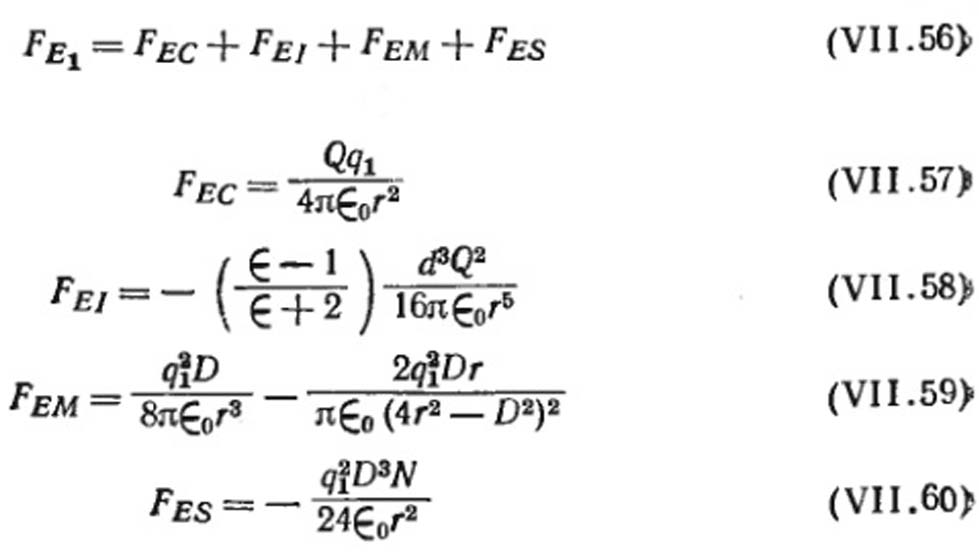
где Q и q_i - соответственно заряд коллектора и частицы; r - расстояние между частицей и коллектором; N - объемная концентрация частиц; Ҽ и Ҽ₀ - диэлектрическая проницаемость, соответственно частицы аэрозоля и пространства (Ҽ₀ = 8,85 ˟ 10⁹А/(Н˟м²).

Если к сферическому коллектору приложено постоянное напряжение U₁ то необходим еще один добавочный член F_ET в выражении для общей силы F_E2 между частицей зарядом и общим зарядом, индуцированным на коллекторе всеми окружающими eго в радиусе R частицами:

F_E2 = F_EC + F_EI + F_EM + F_ES + F_ET (VII .61)

В этом уравнении составляющие силы, выраженные через напряжение U₁, записываются в виде:


Эти силы выражаются через безразмерные параметры К, получаемые путем деления сил в приведенных выше уравнениях.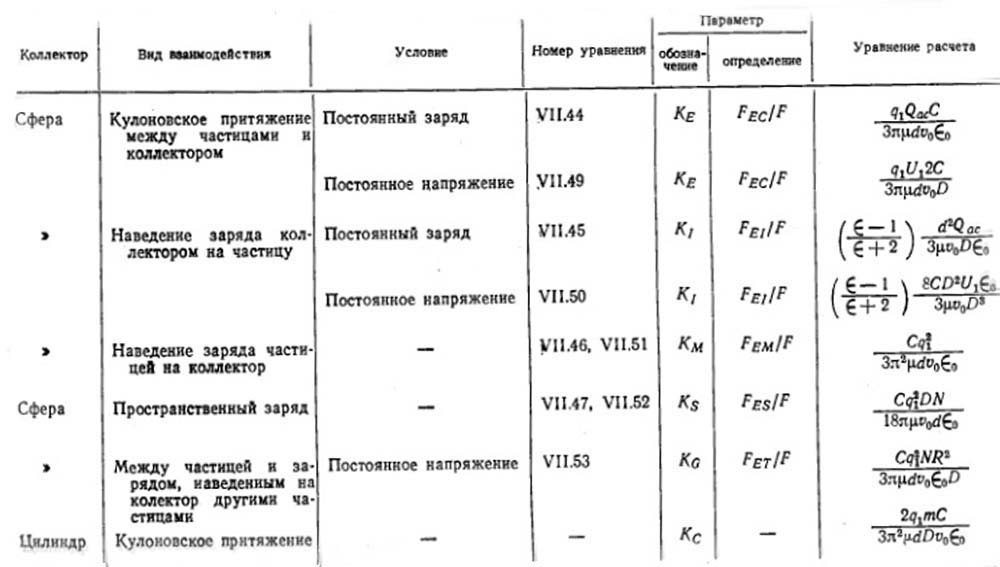

Таблица VII-3. Параметры электростатических сил.

Таблица VII-4. Приближенные значения эффективностей улавливания.

Примечание. Для всех видов коллекторов - заряд несет и коллектор, и аэрозоль. Исключение составляют коллекторы, отмеченные звездочкой - для них заряд несет только коллектор силу в уравнении Стокса - Канингхема F = 3πμdv₀/C (уравнение (IV.34)). Параметры сил и их определение приведены в табл. VII-3.

Приближенные уравнения для расчета эффективности улавливания могут быть получены только в том случае, если учитывается только один член из уравнения электростатических сил (уравнение (VII.56) или (VII.61)) и при условии, что параметр перехвата R = 0. Приближенные решения приведены в табл. VII-4.

Однако эти решения очень ограничены. В них не учитывается совместное действие двух или более форм электростатических сил; они не могут применяться в случае незаряженного коллектора, в них не учитывается эффект перехвата. Более того, оценка эффективности улавливания основана на разумных предположениях только в том случае, когда эффективности намного больше единицы (под эффективностью понимают отношение величины Ilim к фронтальной площади коллектора).

Натансон рассматривал также наличие кулоновских и поляризационных сил взаимодействия между частицами и цилиндром и вывел уравнения для эффективности захвата, подобные уравнениям Кремера и Джонстона. Они были рассмотрены в обзоре Пича и здесь приводиться не будут.

Гораздо более реалистические решения были получены при рассмотрении полного баланса сил для частиц и с учетом соотношений для линий тока вокруг коллектора как при потенциальном, так и вязком течениях. Эти решения были получены на ЭВЦМ.

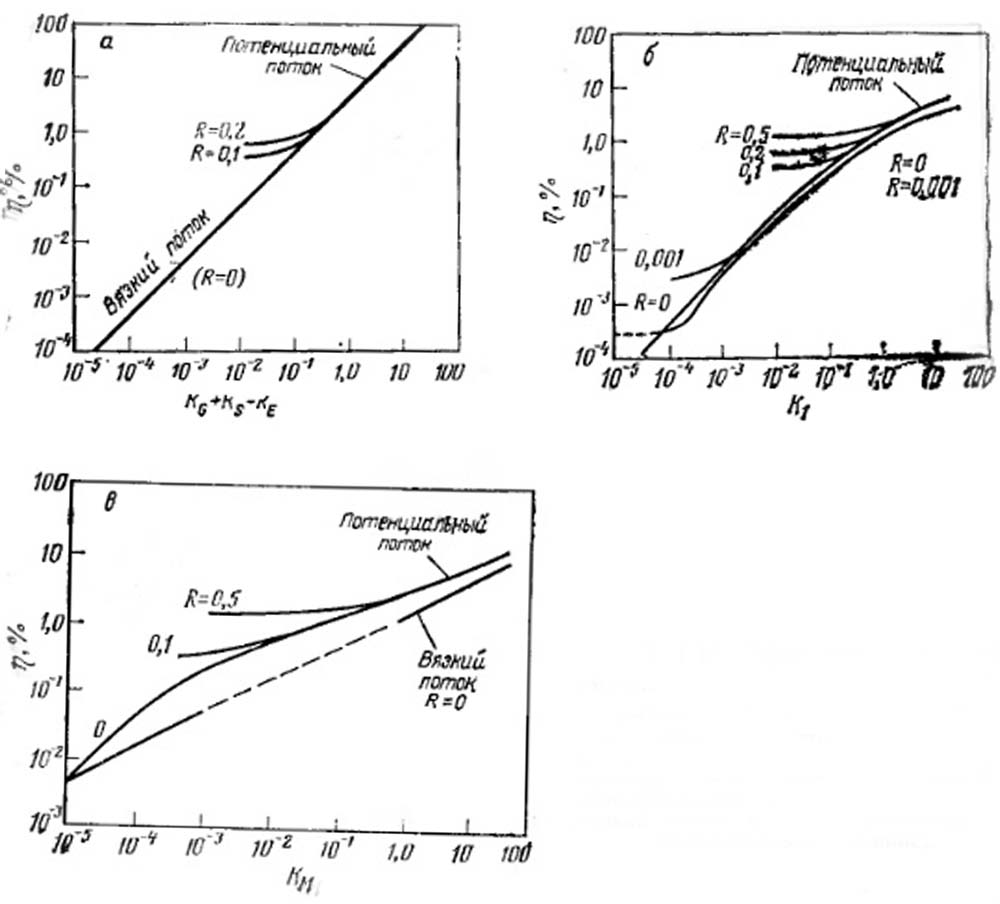
Рис. VII-15. Эффективность улавливания сферических частиц сферическим коллектором.

а - заряжены н частицы и коллектор; б - заряжен коллектор; в - заряженые частицы; 1 - потенциальный поток; 2 - потенциальный и вязкий поток; 3 - вязкий поток (кривые рассчитаны на вычислительной машине).

Здесь же представлены графики для трех возможных случаев, когда заряжены и частицы, и коллектор (рис. VII-15,а), когда заряжен коллектор, а частицы нейтральны (рис. VII-15, б) и когда не заряжен коллектор и заряжены частицы (рис. VI1-15,в).

Эти расчеты дают меньшие значения эффективностей, чем значения, рассчитанные путем суммирования приблизительных эффективностей для различных механизмов. Разница колеблется между 1 и 25% и в среднем составляет около 5%. Экспериментальные результаты хорошо совпадают с теоретическими (рис. VII-16), хотя при низких значениях эффективности они не учитываются теорией.

Расчеты и эксперименты показывают, что эффективность намного выше тогда, когда заряжены и частицы, и коллектор; пылеулавливание улучшается даже в тех случаях, когда заряжен только один из элементов. Джиллеспай показал, что электростатический заряд увеличивает размер частиц для максимального проникновения в слой фильтра (рис. VII-17). Это отчасти может служить объяснением аномальности результатов, полученных Хэмфри и Гаденом, которые нашли, что размер для максимального проникновения спор В. subtilis, несущих некоторый электростатический заряд, составляет 1,15 мкм. Эта величина больше, чем можно было бы ожидать, исходя из рис. VII-11, как для теоретического, так и для экспериментального максимумов.

Лундгрен и Вайтби получили эмпирические уравнения для эффективности осаждения частиц с большим электростатическим зарядом на основе экспериментов с частицами метиленового голубого диаметром 1 мкм. Они нашли, что эффективность фильтра из шерстяного фетра, составлявшая 16% для незаряженных частиц, достигала более чем 99%, когда частицы приобретали элементарный заряд. На основании этого Лундгрен и Вайтби предложили следующее уравнение для расчета эффективности осаждения заряженных частиц на незаряженном фильтре при Re < l.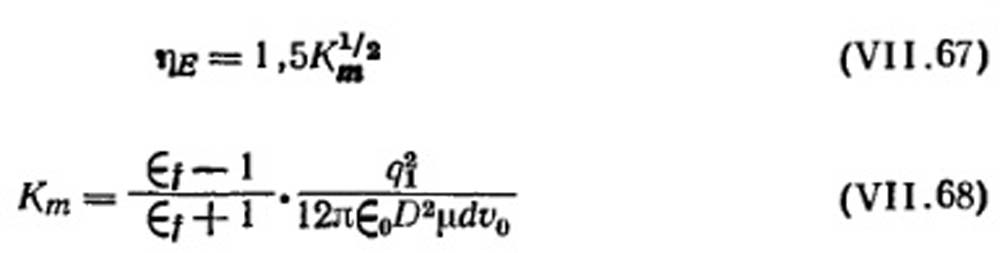

Ҽ1 - диэлектрическая проницаемость волокна. Остальные обозначения имеют тот же смысл, что и в уравнении (VI 1.56).

В обзоре Леффлер подчеркивает, что эти исследователи, а также Джиллеcпай пришли к выводу, что электростатические силы не имеют большого значения в случае крупных частиц, так как здесь доминирующими являются силы инерции, но становятся основным фактором в случае улавливания частиц субмикронных размеров.

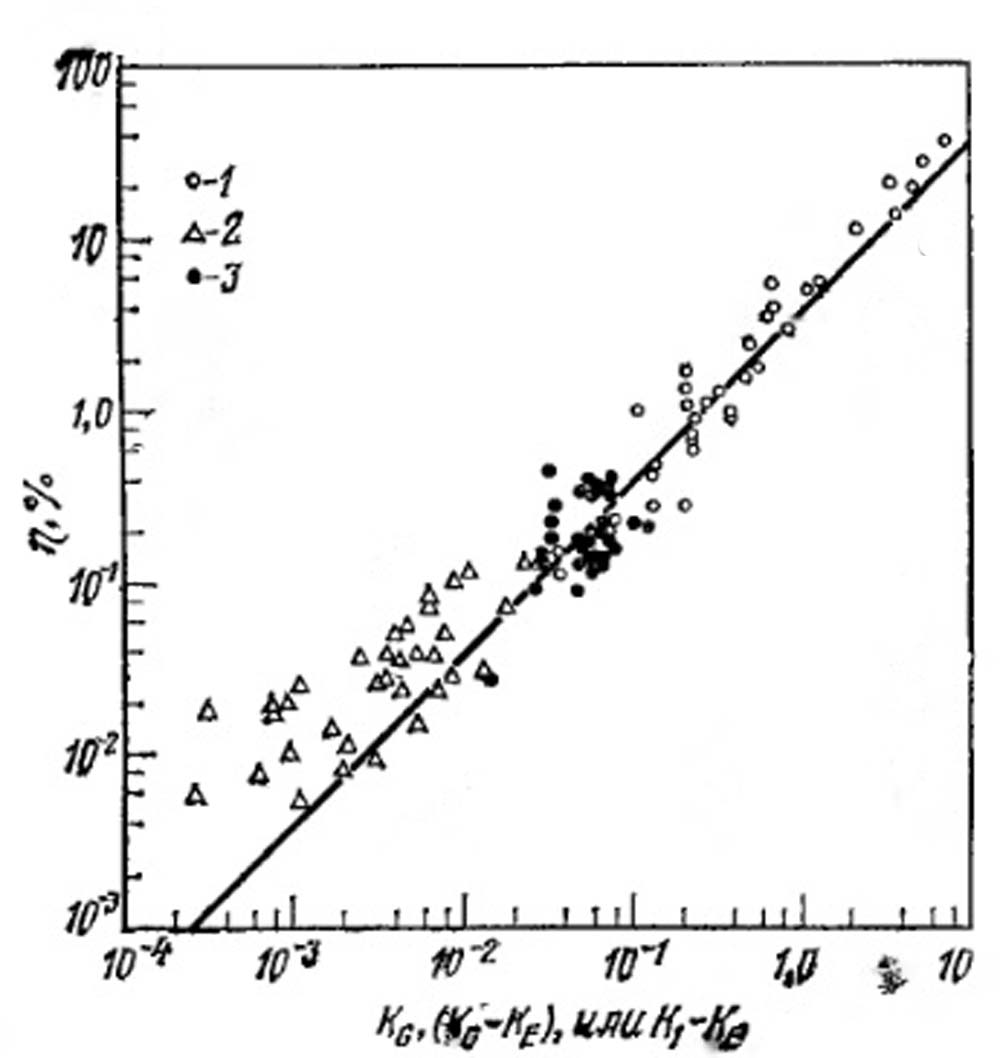
Рис. VII.16. Сравнение теоретических и экспериментальных результатов при улавливании аэрозоля диоктилфталата на сферическом коллекторе.

1 - заряженный коллектор, аэрозоль заряжен в коронарном разряде, параметр (K_G - K_E); 2 - коллектор заряжен, аэрозоль с естественным зарядом, параметр (К₁ - К_Е); 3 - коллектор - аэрозоль заряжен в коронарном разряде, параметр K_G сплошная линия - теоретическая кривая.

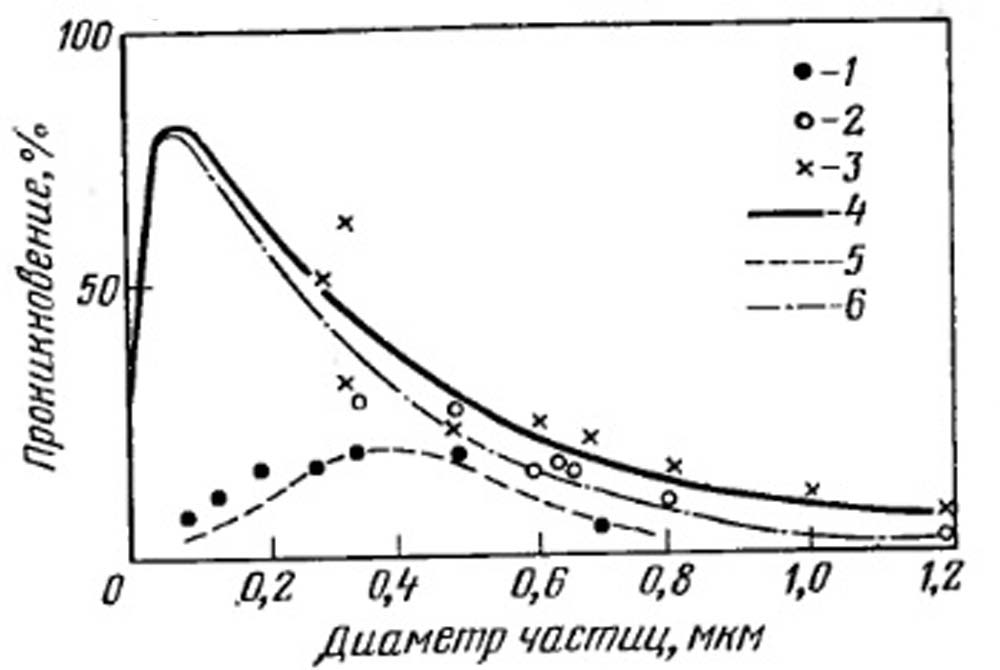
Рис. VII-17. Электростатические силы, влияющие на диаметр частиц для максимального проникновения (поверхностная скорость газа 113 мм/с).

1 - 3 - экспериментальные данные; 1 - заряженный аэрозоль - заряженный фильтр (частицы полистирола - облученное синтетическое волокно); 2 - незаряженный аэрозоль - заряженный фильтр (стеариновая кислота - облученное синтетическое волокно); 3 - незаряженный аэрозоль - незаряженный фильтр (стеариновая кислота синтетическое волокно); 4 - 6 - расчетные данные; 4 - гетерогенный заряженный аэрозоль заряженный фильтр (420 В/м); 5 - гомогенный аэрозоль - заряженный фильтр (420 В/м); б - гомогенный аэрозоль - незаряженный фильтр.