Диффузия

Диффузия

Очень маленькие частицы, размеры которых лежат в субмикронной области, редко могут быть уловлены путем инерционного столкновения или перехвата, поскольку они не только следуют по линиям тока, обтекающим улавливающее тело, но и беспорядочно пересекают их. Это неупорядоченное, зигзагообразное движение маленьких частиц, обусловленное их постоянными, хаотическими столкновениями с молекулами газа, называется броуновским движением.

В покоящемся газе маленькие частицы движутся свободно и распределяются по всему объему газа. Если в газ поместить какой-нибудь предмет, некоторые частицы будут оседать на нем, таким образом удаляясь из газовой среды. В движущемся газе время, в течение которого может происходить такой диффузионный процесс удаления частиц, ограничено, т. е. оно определяется периодом, пока линии тока газа, из которых происходит диффузия частиц, находятся достаточно близко от улавливающего тела.

Оценка количества частиц, удаленных из газа за время, пока газовый поток проходит через пылеуловитель, может производиться одним из методов. По методу, введенному Лэнгмюром, рассчитывают среднее расстояние, пройденное диффундирующей частицей за это время, и эффективность улавливания определяется путем сравнения объема газа, очищенного диффузией, с общим объемом газа, прошедшего через пылеуловитель. По другому методу эффективность улавливания определяют на основе теории массопереноса, рассчитывая скорость диффузии через пограничный слой за период времени, пока газ, из которого происходит диффузия частиц к поверхности, находится достаточно близко от нее.

В первом методе Лэнгмюр рассчитал, используя теорию «случайных блужданий», что слой покоящегося газа, очищенный от частиц, диффундирующих к поверхности, может быть найден из уравнения:

х = (4D_дt/π)^1/2 (VII. 21)

где D - коэффициент диффузии частиц.

Коэффициент диффузии частиц может быть найден двумя путями. Один из них, предложенный Эйнштейном, применим для частиц, размеры которых равны или превышают среднюю длину свободного пробега молекул газа. Другой, введенный Лэнгмюром, применим для частиц размером меньше длины свободного пробега. Эйнштейн, рассматривая осмотические силы, установил, что коэффициент диффузии может быть найден из соотношения:

D_д = kT/F' (VII.22)

где k - константа Больцмана; Т - абсолютная температура; F' - сопротивление среды, равное трем.

Для размеров частиц такого порядка, которые могут удаляться из газового потока путем диффузии, сопротивление среды может быть выражено законом Стокса с поправкой на "проскальзывание" (поправочный коэффициент Каннингхема С), тогда уравнение (VII.22) записывается в виде

Dд = CkT/3πμd (VII.23)

Лэнгмюр использовал теорию диффузии Стефана - Максвелла, в которой предполагалось, что частицы не влияют на молекулы газа. Это ограничивает область применения коэффициента диффузии, рассчитанного по этой теории, до частиц таких размеров, которые намного меньше среднего свободного пробега молекул газа, но значительно больше размеров самих газовых молекул. Лэнгмюр нашел, что коэффициент диффузии может быть определен из соотношения:

D_д = u/3N(πd²/4) (VII.24)

где N - число молекул газа в единице объема; u - средняя скорость молекул.

Таблица VII. Коэффициенты диффузии частиц и числа Шмидта.

Коэффициенты диффузии частиц и числа Шмидта (воздух при 20°С и давлении 100 кПа).

Число молекул газа в единице объема зависит от давления газа, т. е. N=P/kT для обычного давления, когда соблюдаются законы идеальных газов. Заменяя N и u в уравнении (VII.24) их значениями для коэффициента диффузии, получаем:

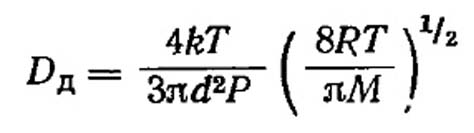(VII.25)

Некоторые коэффициенты диффузии, рассчитанные как из уравнения (VII.23), так и из (VII.25), приведены в табл. VII.1.

Если давление выражено в Па, коэффициент диффузии измеряют в м²/с. Число Шмидта Sc является безразмерной величиной, включающей коэффициент диффузии: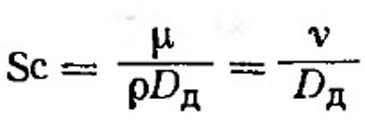
(VII.26)

где v=μ/р - кинематическая вязкость.

Числа Шмидта, соответствующие коэффициентам диффузии частиц, также приведены в табл. VII-1.

Другой безразмерной величиной, используемой в таких вычислениях, является число Пекле (Ре), которое представляет собой меру переноса за счет конвекции по сравнению с переносом за счет молекулярной диффузии. Для системы, в которой газовый поток со скоростью v движется мимо тела диаметром D, число Ре записывается в виде:

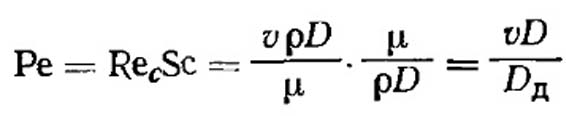(VII.27)

Биллингс указывает, что решения, предложенные для определения эффективности улавливания путем диффузии, можно приближенно записать в виде:

ȵ_D ~ Re^-n

где 1/2 ≤ n ≤1 , тогда как общепринято, что правильное теоретическое значение, вероятно, получают при n = 2/3. Рис. VII-7. Диффузионная область вокруг улавливающего тела.

Решения зависят также от логарифма числа Рейнольдса для цилиндра Rec, хотя его влияние в области 10^-4 ≤ Re_c ≤ 10^-1 мало.

Лэнгмюр предположил, что диффузия будет происходить из поверхностного слоя эффективной толщины хе в течение времени t, за которое элемент потока пройдет от точки 1 до точки 2, выбранных на пересечении, образующем угол 60° с набегающим потоком и угол 60° с уходящим потоком по отношению к улавливающему цилиндрическому телу.

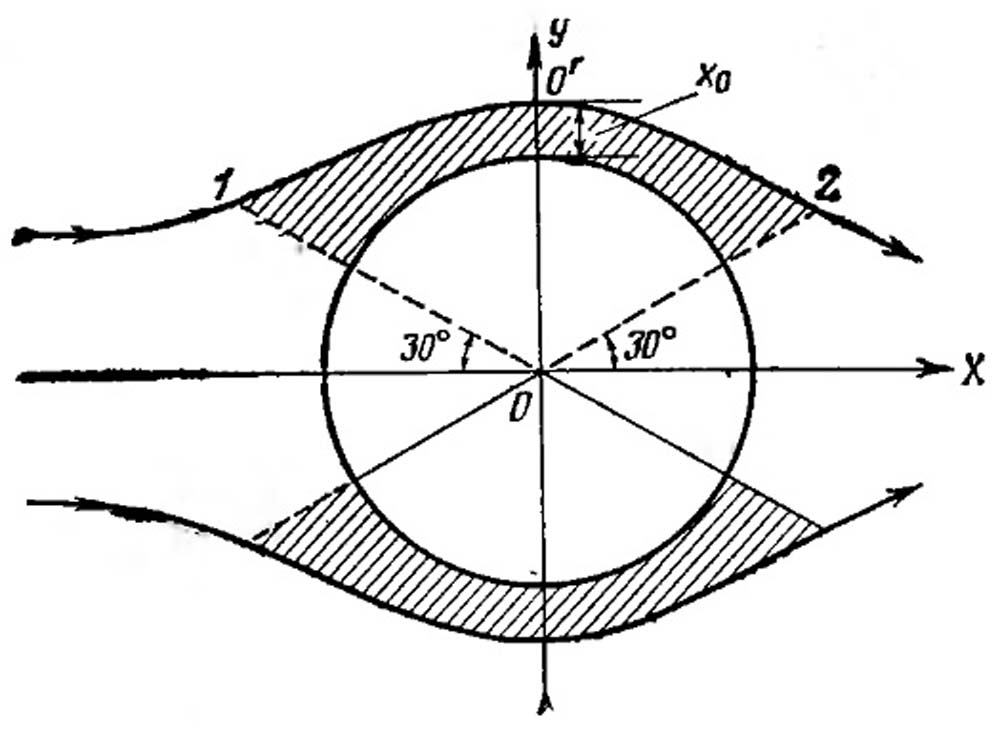
Рис.VII-7. Диффузия вокруг улавливающего тела.

В точке О' элемент потока находится на расстоянии х₀ от улавливающего тела. На основании постадийного интегрирования уравнения для вязкого течения вокруг цилиндра было найдено эффективное расстояние х_е в первом приближении:

х_е= 1,12х₀ (VII.28)

Время, за которое элемент потока пройдет от точки 1 до точки 2.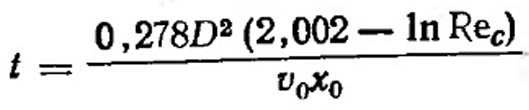
(VII.29)

Эти значения t и х_о можно подставить в уравнение (VII.21) и после перегруппировки найти параметр диффузии Z (подобный параметру перехвата).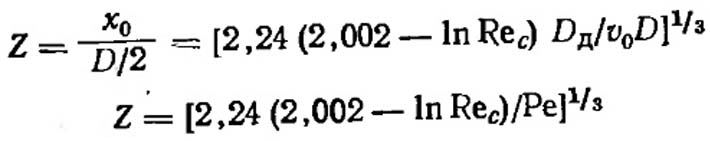
(VII.30),(VII.31)

Лэнгмюр указал, что более строгий подход к расчету диффузии привел бы к изменению коэффициента 2,24, но мало вероятно, что это изменение будет значительным. Впоследствии Натансон предположил 593, что коэффициент 2,24 должен быть примерно в два раза больше, чем у Лэнгмюра.

Теперь эффективность улавливания путем диффузии может быть рассчитана из уравнения Лэнгмюра для эффективности улавливания путем перехвата (VII.16):

Таблица VII-2. Числа Пекле и эффективность диффузионного улавливания для волокон диаметром 1 мкм при скорости потока 0,1 м/с (воздух при 20 °С и 100 кП)

Эффективность улавливания, рассчитанная для частиц, движущихся около волокна диаметром 1 мкм в газовом потоке со скоростью 0,1 м/с, приведена в табл. VII-2.

Натансон вывел следующее уравнение для ламинарного потока и чисел Пекле Ре<1: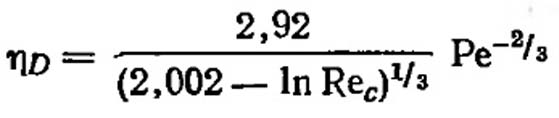
(VII.33)

Фукс и Стечкина вывели уравнение для эффективности осаждения, основанной на соотношении Кувабары - Хаппелл.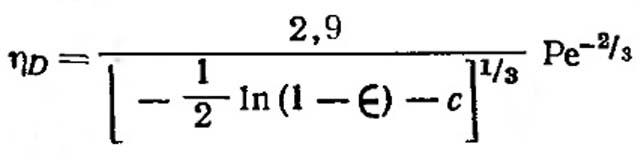
 (VII.34)

где все обозначения те же, что и в уравнении (VII.5).

Бозанке использовал подобный подход, не предполагая, что расстояние контакта равно половине периметра (π_D/2) и получил уравнение для эффективности улавливания цилиндрическим телом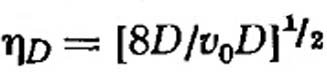
(VII.35)

Эффективность улавливания, рассчитанная по уравнению (VII.35), также приведена в табл. VII-2.

Точно таким же образом можно рассчитать эффективность улавливания для сферы и для одной стороны полосы шириной W, ориентированной под прямым углом к газовому потоку: для сферы: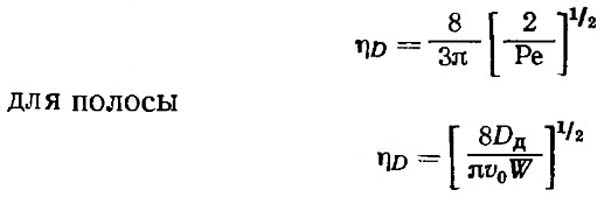
(VII.36),(VII.37)

Из-за ряда чисто математических затруднений расчет эффективностей улавливания на основе соотношений массопереноса не был полностью разработан. Общее уравнение для массопереноса в неустановившемся состоянии, обычно называемое законом Фика, записывается в виде:
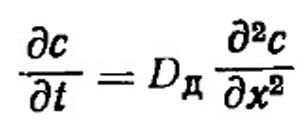 (VII.38)

где с - концентрация частиц; х - толщина слоя непосредственно вокруг улавливающего тела.

Если не происходит накопления частиц в этой зоне, то уравнение (VII.38) можно интегрировать и получить скорость диффузии частиц на единицу площади улавливающей поверхности.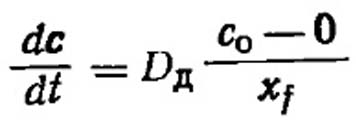
(VII.39)

где x_f - толщина зоны вокруг улавливающего тела, в которой существует градиент концентраций; с_о -концентрация частиц в объеме газа; О - концентрация на поверхности коллектора.

Джонстон и Робертс предположили, что для расчета эффективности диффузионного улавливания в случае сферического улавливающего тела можно использовать коррелирующую функцию, аналогичную корреляции для теплопереноса.

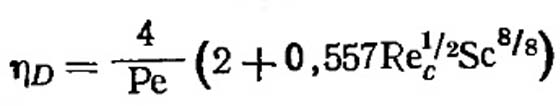(VII.40)

Позднее Ранц дал аналогичную формулу для цилиндров которую используют для условий 0,l < Re < 104 и значений Sc < 100.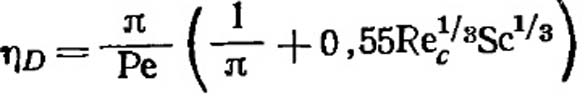
(VII.41)

Ланд предположил, что эффективность диффузионного улавливания может быть найдена из π/Ре, в то время как Дэви считал, что величина, обратная числу Пекле (1/Ре), приведет к таким же значениям эффективности, что и соответствующие значения параметра инерционного столкновения f. Однако последнее предположение не позволило получить реальных оценок для улавливания путем диффузии (см. табл. VII.2).

Горен ссылается на Стечкину, предложившую следующее уравнение для улавливания путем диффузии которое основано на уравнении (VII.4).

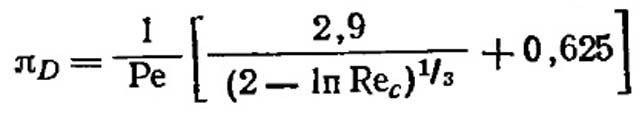(VII.42)

Штерн провели эксперименты по определению эффективности улавливания субмикронных частиц полистирола на фильтре при пониженных давлениях, когда диффузия является превалирующим механизмом. Эти исследователи использовали уравнение Торгесона: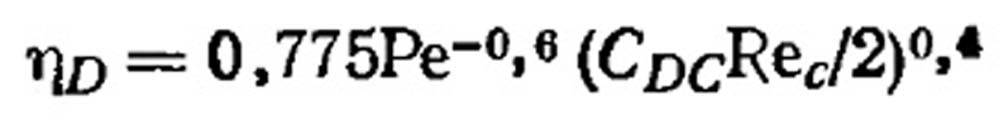

 (VII.43)

где C_DC - коэффициент лобового сопротивления волокна.

Величины C_Dc и Re характерны для данного фильтра, их находят экспериментально, зная перепад давлений ∆р, удельный объем волокна α и толщину фильтра h, из формулы Чена.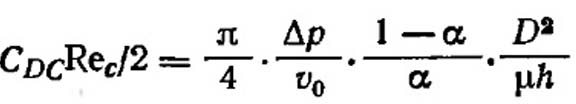
(VII.44)

Эффективность диффузионного улавливания на основе уравнения Лэнгмюра приблизительно в два раза ниже значений, полученных из уравнения Торгенсона. Однако к этим результатам следует относиться с осторожностью. Например, при Ре = 36 эксперментальное значение ȵD составило 50%, тогда как по оценке Торгенсона получили 35%, а по уравнению Лэнгмюра 18% улавливания. При приблизительной интерполяции данных Штерна для Ре = 163 экспериментальная эффективность составит 18%, тогда как по уравнению Лэнгмюра 3% (с использованием уравнения диффузии Эйнштейна) или 6% (при использовании уравнения диффузии Лэнгмюра), по уравнению Бозанке получают 22%, а по уравнению Торгесона - около 15%.

До тех пор, пока не станут доступными более расширенные экспериментальные данные и, если имеется мало информации о свойствах фильтрующей среды, можно пользоваться либо уравнением Лэнгмюра (VII.32), либо уравнением, аналогичным уравнению теплопереноса (VII.41). Если для данного фильтра можно найти данные о перепаде давлений, плотности фильтра, размерах волокон и толщине слоя, то наиболее надежная оценка может быть получена при использовании уравнения Торгесона.

Лэнгмюр видоизменил свои уравнения (VII.28) - (VII.32) Для сочетания перехвата и диффузии. Эффективная толщина полосы, которая очищается от частиц, на самом деле на d/2 больше, чем х в уравнении (VII.31). Из-за других сделанных допущений эта поправка не всегда оправдана, за исключением тех случаев, когда площадь поверхности коллектора становится очень большой.